Have an AWEsum Fibonacci Day!
Imagine a moment — let’s call it an awe moment — when something took your breath away, caught you off guard or surprised you. It might have been a song you heard, a play or movie you saw, a poem or book you read, a sunrise or sunset you saw, an encounter with nature, a spectacular meal you had or a magic show that left you speechless. Can you imagine what life would be like without having awe moments? In fact, researchers have explored the benefits of awe and have found that it is good for us!
Eight reasons why awe makes your life better
In this
article by Summer Allen, research suggests that awe can make you happier, healthier,
humbler and more connected to the people around you.
Now imagine an encounter with mathematics that left you awestruck. For teachers, this is probably not a hard thing to do. After all, many of us are in love with mathematics and we love to teach the subject. But how would students respond to this? Are they ever in awe of the beauty or power of mathematics? Do they encounter things that are surprising or mysterious? If the answer is generally no, then how can we expect them to want to learn more? Without having an occasional moment of awe, going to their mathematics classes must be an awe-ful (awe-less?) experience for these students.
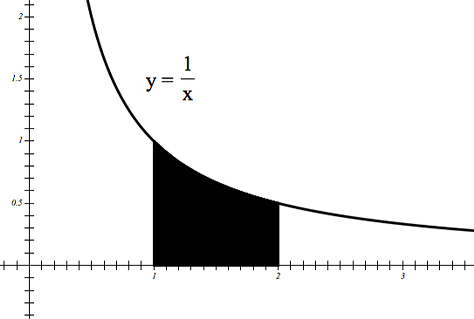
I vividly remember a high school teacher who told us that the area of the region shown in figure 1 was equal to the natural logarithm of 2. We had not yet studied how to calculate the area between two curves, and I was blown away by this result. I could not imagine how logarithms were involved in calculating this area. It wasn’t until several years later that I understood why, when I was studying integral calculus. Then it was obvious why the area was equal to ln(2), but I could still feel the magic in this result. Maybe there is a lesson here for teachers. Why not expose students to results that are full of intrigue and mystery before they have the mathematical background to understand the result? For some students, this will motivate them to want to learn more mathematics.
November 23 is Fibonacci Day. The Fibonacci sequence (defined below) is a golden source of results and relationships
that can be the makings of awe moments for your students. Here are three examples for you to share with your
students.
Awe moment number 1
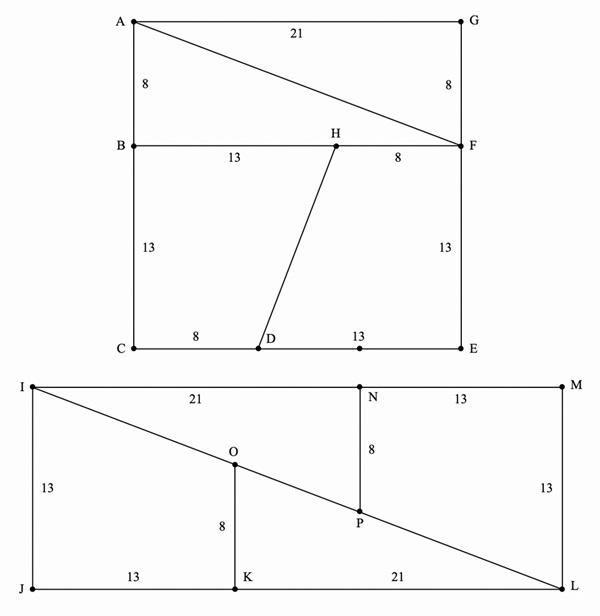
The square shown below has been divided into two congruent trapezoids and two congruent triangles. These trapezoids
and triangles were used to make the rectangle shown below (figure 2). The length of the side of the square is 21
units and so its area is 441 square units. The length of the rectangle is 13 units and the width is 34 units. So the
area of the rectangle is 442 square units. But this is impossible! The area of the square has to be the same as the
area of the rectangle. Provide several different ways of explaining this mystery.
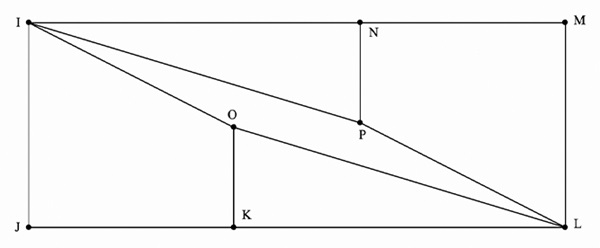
If you or your students have never seen this before, it surely will come as a surprise, especially if you cut out the pieces and see that they really form the square and rectangle. Well, actually they do not! This is an example of a geometric dissection, popularized by Martin Gardner. You can take the varnish off the vanish by using mathematical topics that include similar triangles, slope and trigonometry. Although the scale is exaggerated, figure 3 shows what is really happening: The diagonal of the rectangle (line segment IL) is actually a long and thin parallelogram whose area is equal to 1 square unit.
Here is another surprise. Look at the numbers in the diagram: 8, 13, 21. These are three consecutive terms of the
Fibonacci sequence. You can create additional geometrical vanishes using any three consecutive terms of the
Fibonacci sequence! But why is the Fibonacci sequence involved? Well, it is because of a beautiful relationship
between any three consecutive terms of the Fibonacci sequence. Pick a term and square it. Multiply the term before
the one you selected by the term after it. The product is always one less or one more than the square. Try it!
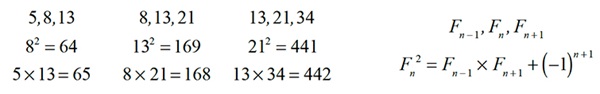
Readers are invited to find a formula for the height of the parallelogram as a function of terms of the Fibonacci sequence and then to show that the height tends to 0 as n tends to infinity.
Awe moment number 2
Let a and b be the roots of the quadratic sequence x2 - x - 1 = 0.
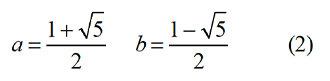
Note that a2 - a - 1 = 0 and so a2 = a + 1. Therefore
a3 = a2 + a, so a3 = 2a + 1. Similarly
we have b3 = 2b + 1. If
we continue to express powers of a and b in terms of a and b, the Fibonacci
sequence makes a surprising appearance.
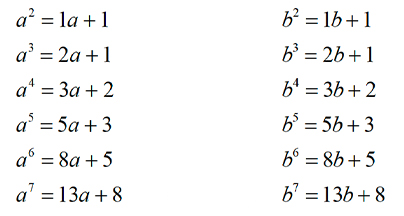
It seems that
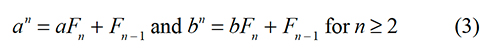
Assuming that this is true, here is a shocking result: an explicit formula for the nth term of the Fibonacci
sequence
that involves the roots of a quadratic equation.
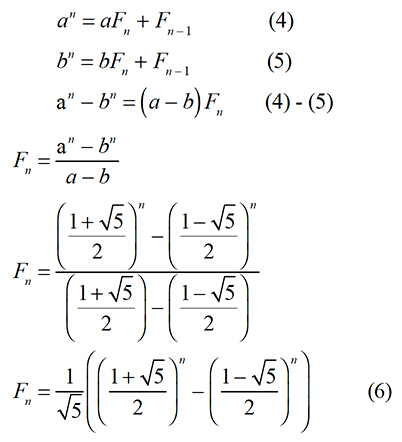
Equation (6) is another one of the results that my high school teacher showed our class. I remember being stunned by this result — I could not imagine how the Fibonacci sequence was related to the square root of 5 and how one would go about developing this explicit formula. I wanted to learn more, and this is precisely the point of this blog. Of course, not all your students will react this way, but there are those who will have the same type of seismic experience that I did.
There remains the issue of showing that the result given below is true.
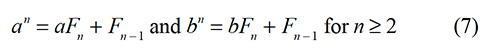
One way of doing this is to let
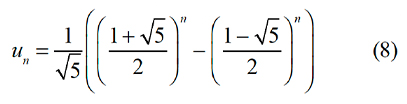
and then show that
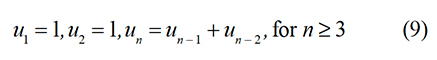
We will then be able to conclude that un is the Fibonacci sequence. The proof does not require advanced algebraic skills — one needs to be careful and organized. This is a good exercise for some of your students.
The explicit formula for the nth term of the Fibonacci sequence given in (6) is known as Binet’s Formula. Although a TI-84 Plus CE-T family graphing calculator does not have a Computer Algebra System (CAS), it does a remarkable job of calculating terms of the Fibonacci sequence up to the 49th one using Binet’s Formula (figure 4). The TI-Nspire™ CX CAS graphing calculator is able to calculate the nth term of the Fibonacci sequence all the way up to n = 255 (figure 5). Whoa!

Awe moment number 3
Write down the first ten terms of the Fibonacci sequence: F1, F2, F3, ..., F10.
Find the least common multiple of the first ten terms.
Calculate of the product of the first ten terms.
Which number is bigger: the least common multiple of the first ten terms or the product of the first ten terms? How
do you know?
Both the least common multiple and the product are big numbers, so let’s cut them down in size by taking the
logarithm of both of them. Use whatever base comes naturally to you.
Consider the fraction given below. Note that lcm and product represent the least common multiple and the product of the numbers listed within the brackets. For example, lcm(8, 12, 30) = 120 and product(8, 12, 30) = 2,880.
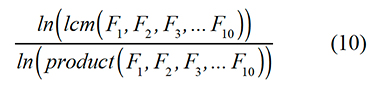
Is this fraction less than, equal to, or greater than 1? Does the answer depend on which base you use for the logarithm? Why or why not?
Use a TI-84 Plus CE-T or TI-Nspire™ CX family graphing calculator to convert the fraction to decimal form.
So far this is not particularly interesting. But here is a question that leads to another surprise. How does the value of the fraction given above change if we use the first 20 terms of the Fibonacci sequence (instead of the first ten), or the first 30 terms, and so on? If we use the first n terms of the Fibonacci sequence, does the value of the fraction shown below have a limit as n tends to infinity? How could you determine a numerical approximation to the limit of tn if it exists?
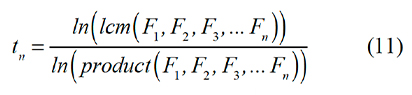
It is not hard to find the lcm and the product by hand for n = 10. But larger values of n demand the use of technology.
Let’s take a look at what happens when the TI-84 Plus CE-T family graphing calculator is used to find the lcm and the product of the first 10 terms (figure 6).
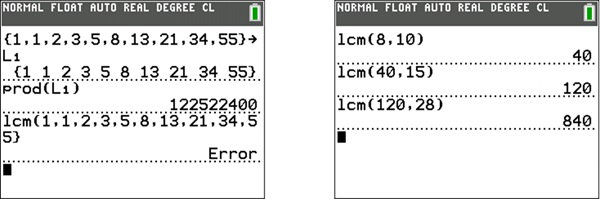
A TI-83 Premium CE or TI-84 Plus CE-T family graphing calculator is able to calculate the product of the first 10 terms, but an error arises when an attempt is made to find the lcm of the first 10 terms. The TI-83 Premium CE, TI-84 Plus CE-T and TI-Nspire™ CX II-T families of graphing calculators are limited to finding the lcm of only two numbers. One way of finding the lcm of more than two numbers using the TI-83 Premium CE, TI-84 Plus CE-T and TI-Nspire™ CX II-T families of graphing calculators, is by doing it in steps (figure 7). However, this is certainly not very efficient.
In order for your students to make a conjecture about the limit of tn, suggest to them that they write a TI-Basic or Python program that calculates tn for large values of n. In order to write the code, they will need to figure out the coding for calculating the lcm of a set of numbers.
The details are too complicated to get into here, but I can tell you that the sequence tn does have a limit and it converges very slowly. Here are the first 20 decimal places of the limit: 0.60792710185402662866...
Are you sitting down? I ask because I have something to tell you about these 20 decimal places that may come as a shock to you and leave you in a permanent state of awe. They are the first 20 decimal places of the number given below.
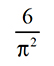
Here is what equation (11) looks like when we add in the limit.
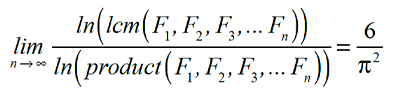
This has to be one of the most bizarre results that I have ever seen. What does π have to do with the Fibonacci sequence? If your students want to understand the connection between the Fibonacci sequence and π, tell them to keep studying mathematics.
I found this limit on page 115 of the second edition of one of my all-time favorite books, “Fibonacci and Lucas Numbers With Applications” by Thomas Koshy. This hardcover book is over 600 pages long and contains a gold mine of material about the Fibonacci sequence. Add this book to your library or the library at your school. Koshy found the limit in this article, Matiyasevich, Yuri V. “A New Formula for π.” Published in The American Mathematical Monthly 93, no. 8 (Oct. 1986): pp. 631–35.
This is how the limit appeared in the article. Note that the author referred to the product of a set of numbers as the full common multiple (fcm). I rewrote the limit in a different form so that it would be equal to 6/π2.
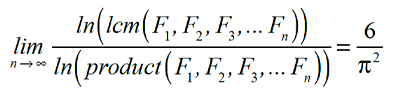
At the risk of overloading you with too much awe, I have two last things to share with you.
Item 1
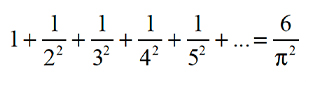
Item 2
The probability that two positive integers selected at random are relatively prime, is equal to 6/π2.
You have seen three examples where the number 6/π2 makes an appearance. If this is not an OMGoodness moment, I do not know what is. If your students want to know how it is that the Fibonacci sequence, the sum of an infinite series and relatively prime numbers are all connected to π, tell them to take more mathematics courses.
Happy Fibonacci Day to all of you! I was thinking of ending with another joke, but you probably would have said it was as bad as the last two you read combined.
About the author: Ron Lancaster is an Associate Professor, Teaching Stream, Emeritus at the University of Toronto where he taught mathematics courses for pre-service middle and high school teachers for 17 years. Before joining the faculty of the University of Toronto, Lancaster taught middle and high school mathematics for 23 years in coed public schools and a K–12 all-girls school.
